题目总数：24 总分数：100
第 1 题 单选题
下列关于 2024 年海淀区信息学比赛(初赛)的说法，错误的是( )
A.
在海淀区初赛中成绩达到一定标准才能晋级，获得参加海淀区信息学复赛的资格。
B.
海淀区初赛是笔试，全部是选择题，必须把正确答案按要求填涂在答题卡的指定位置上。
C.
监考老师会通知考生:考试结束后考生要在监考老师的带领下到操场上指定的区域与家长对接。
D.
不管是谁只要想参加都可以报名。
第 2 题 单选题
假设浮点类型变量 x 已定义并赋值，那么int(x)的作用是( )
A.
向上取整
B.
向下取整
C.
去掉小数点及小数部分
D.
四舍五入
第 3 题 单选题
设 int x=1,y=2，则表达式:(++x)+(y++)输出的结果为( )
A.
2
B.
3
C.
4
D.
5
第 4 题 单选题
下列有关提高穷举算法效率的方法中，说法错误的是( )
A.
通过推导，减少穷举的范围和数量能提高穷举算法效率。
B.
通过预处理，避免重复的计算发生能提高穷举算法效率。
C.
用更小规模的函数分解现有函数能提高穷举算法效率。
D.
以空间换时间，避免重复的判断发生能提高穷举算法效率。
第 5 题 单选题
下列有关选择排序算法的叙述中，正确的是( )
A.
选择排序算法是不稳定的排序算法。
B.
对于同一数列，选择排序的速度快于冒泡排序。
C.
直接选择排序算法的时间复杂度为 O(n)。
D.
选择排序算法数据总的比较次数与关键字序列的初始状态相关。
第 6 题 单选题
一个 int 类型的数，做以下哪个操作，一定能变回原来的值?( )
A.
左移 3位再右移 3 位
B.
右移3位再左移 3位
C.
按位异或7再按位异或7
D.
按位或7再按位与 -8
第 7 题 单选题
如果 x 为 char 类型的变量 ，下列选项符合 C++ 语法且能正确判断x 是小写字母的是( )
A.
x-'a'<= 26
B.
'a'<= x <='z'
C.
'a'<==' x='<='z'
D.
('a'<= x )&&(x<='z')
第 8 题 单选题
以下数据结构中，属于非线性数据结构的是( )
A.
字符串
B.
树
C.
数组
D.
队列
第 9 题 单选题
已知字符集 {a,b,c,d,e,f,g,h}，如果给每个字符进行编码，字符与编码对应如下!
则编码序列 0100011001001011110101 的译码结果分别是( ）
A.
e,c,g,e,b,f,h
B.
e, d, b,e, g, b,b
C.
e, f, b, a,e,g,d
D.
e, f,a,a,f,g,d
第 10 题 单选题
一种常用的数据结构栈是只允许在一端进行进栈(插入)或出栈(删除)操作的线性表。如果进栈序列为 1,2,3,4,5 ，则出栈序列不可能出现的是( )
A.
5,4,3,2,1
B.
4,3,1,2,5
C.
3,2,1,5,4
D.
2,3,4,5,1
第 11 题 单选题
有两个不相等的浮点数a和b，它们满足关系式a2+3a+1=0，b2+3b+1=0，则a +b的值为( )
A.
-3
B.
-1
C.
1
D.
3
第 12 题 单选题
用符号 ⊕ 表示按位进行异或运算，下列计算的表达式正确的是( )
A.
22|30 的结果是 31
B.
26 &48 的结果是 16
C.
17⊕7的结果是 5
D.
3 &&0 的结果为 2
第 13 题 单选题
甲、乙、丙、丁四人参加冬季滑雪比赛，有一人获奖。在比赛结果揭晓之前，四人作出如下猜测:
甲的猜测:丙会获奖:乙的猜测:我不会获奖;
丙的猜测:丁会获奖;
丁的猜测:获奖者在甲、乙、丙三人之中。
比赛结果公布后表明，四个人中只有一人的猜测是正确的，则下列说法正确的是( )
A.
获奖的一定是甲
B.
获奖的一定是乙
C.
获奖的一定是丙
D.
获奖的一定是丁
第 14 题 单选题
一次比赛共有 1430 人报名，要把他们分成人数相等的若干组，且每组人数在 100 至 200 之间则一共有 ( )种不同的分法。
A.
3
B.
7
C.
9
D.
11
第 15 题 单选题
有5克，25 克，30 克，50 克的砝码各若干个，从中共取 n 个，每类砝码至少取1个，50 克的砝码不能超过6个，若总质量为1千克，则 n 的最小值为( ）
A.
30
B.
31
C.
32
D.
33
第 16 题 单选题
陶陶有5个最要好的朋友，排成一行，从左到右编号从1 到 5，他们每个人手里都至少有一颗糖果。现在陶陶告诉你一些信息，你的任务是根据陶陶给你的信息确定每个人手上的糖果数量。
陶陶给出的信息是:
从1号朋友到5号朋友，对于每个人，他左边糖果数量比他多的人数分别为 0,0,1,1,2，右边糖果数量比他多的人数分别为 2,0,1,0,0。
则下面关于每个人手里糖果数量的推断，错误的是( )
A.
1号糖果数为 1
B.
2号糖果数为 2
C.
3号糖果数为 1
D.
4号糖果数为 2
E.
5 号糖果数为 1
第 17 题 单选题
陶陶邀请了 4 个朋友来参加秋游跑步活动，包括陶陶在内，一共5个人，编号从1到 5，他们约好都穿着跑步鞋，他们的鞋子的型号都有一个不超过5的正整数进行标记，相同的数字代表相同的型号，不同的数字代表不同的型号。
现在每个人都告诉你有多少个人鞋子的型号与他自己的鞋子的型号不同，请你推断各自鞋子的型号可能是多少。
他们告诉你的信息如下:
第 1号人告诉你:有 3 个人的鞋子型号和他鞋子的型号不同;
第 2 号人告诉你:有 3 个人的鞋子型号和他鞋子的型号不同;
第 3 号人告诉你:有 2 个人的鞋子型号和他鞋子的型号不同;
第 4 号人告诉你:有 2 个人的鞋子型号和他鞋子的型号不同;
第 5 号人告诉你:有 2 个人的鞋子型号和他鞋子的型号不同;
则下列按编号从小到大给出的每个人鞋子的型号与他们描述的情况不符合的是( )
A.
2, 2,3,3,3
B.
1, 1,2,2,2
C.
3,3,2,2,2
D.
1,2,1,2,1
E.
2,2,1,1,1
第 18 题 单选题
有 3个男生和 2个女生，每个男生都会给每个女生若干颗糖果。已知3个男生给每一个女生的糖果数量中的最小值分别为 1,2,1，两个女生收到每一个男生给的糖果数量中的最大值分别为 3和 4，则两名女生收到的总糖果数最少是( ）
A.
4
B.
8
C.
12
D.
14
E.
16
第 19 题 单选题
陶陶和聪聪参加班长竞选，一个小组里有6个人，编号从1到6，他们都参加了投票，每个人会在选票上写一个长度为 2的 01 串，投票结束后，记录的这六个人投票的信息依次为:11，10，00，00，11，10。这个 01 串代表的含义如下:
若票上写的是 00，代表这个投票人既不支持陶陶当选，也不支持聪聪当选；
若票上写的是 01 ，代表这个人不支持陶陶当选，而支持聪聪当选；
若票上写的是 10，代表投票支持陶陶而不支持聪聪；
若票上写的是 11 ，代表这个人既支持陶陶，也支持聪聪；
现在知道他们每个人都有一个表示其影响力大小的参数值，分别为 19，22，18，29，29，28。现在请你从中选出若干个人，要求选出的人中支持陶陶的人数的 2倍不小于你选出的人数，支持聪聪的人数的2 倍也不小于你选出人数，则你选出的人的影响力参数值的总和的最大值是( ）
A.
70
B.
105
C.
108
D.
127
E.
145
第 20 题 单选题
定义一个序列的"美丽度"为这个序列中最大的三个元素的总和。
现有一个序列 {5,2,5,2,4,1,1,3,2,6,4,4,5,6,2,2}，请你将这个序列恰好划分为 4个子序列，每个序列长度都不小于3，原序列中的每个元素都在某一个子序列中，且每个子序列都是由原序列中的连续元素构成，则这 4个子序列的“美丽度"之和最大值为( )
A.
45
B.
46
C.
47
D.
48
E.
49
第 21 题 单选题
对于下面的C++程序段，如果输入2则输出的是( ）
#include<bits/stdc++.h>
#define 1l long long
using namespace std;
1l f(int n,int k)
{
11 res=1;
for(int i=1;i<=k;i++)res=res*(n+1-i)/i;
return res;
}
int main()
{
int m;
11 c1,c2;
scanf("%d" ,&m);
c1=f(m+2,3);
c2=f(m+4,5);
printf("%1d",c1*c2);
return 0;
}
A.
8
B.
12
C.
16
D.
24
E.
36
第 22 题 单选题
给你两个长度为 n的数组 a1,a2,...,an 和 b1,b2,..,bn，你的任务是构造一个长度为n 的数组 C1,C2,...,Cn。
要求构造的新数组元素 ci满足 ci = d*α +b，其中i€ [1,n] ，即1≤i<n，这里的d是你指定的一个整数，目标是要使数组c中的 0的个数尽可能多。如果给定的数组a为{1,2,-1,3}，给定的数组b为{-6,-12,6,-9}，则下列说法正确的是( )
A.
数组c中最多有1个0
B.
数组c中最多有2个0
C.
数组c中最多有3个0
D.
当d=3时数组c中会有最多个数的 0
E.
当 d=4时数组c中会有最多个数的 0
第 23 题 单选题
陶陶新学习了二项展开式:
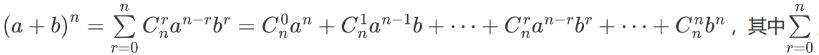是个求和符号，r取值为从0 到 n的每一个整数，
表示从几个不同元素中取出 m(m<n)个元素的不同方法数。陶陶借助该定理计算出了912 mod 103的结果，mod 表示求余运算。以下结果正确的是( )
A.
481
B.
561
C.
721
D.
961
E.
971
第 24 题 多选题
马斯克的火箭公司要造一支新型火箭进行一次火箭旅行，火箭要依次在 6 个行星上降落和起飞,6 个行星的编号从1到6，火箭每次起飞和降落都要消耗一些燃料，已知这支火箭在 6 个行星上起飞的燃料效率分别为 4,6,3,3,5,6，降落的燃料效率为 2,6,3,6,5,3 。
定义火箭一次起飞或者降落的 燃料效率 (p)为火箭本次行动前的火箭总重(m)与本次行动消耗的燃料重量 k的比值，或者把 m,k,p 三者之间的关系描述为 m =k*p，火箭总重为火箭自重与携带的燃料之和。
如果这支火箭自重为 2，只会在起飞和降落行动中消耗燃料，那么它从 1 号行星起飞，依次在每个行星上降落和起飞，过程中不能添加燃料，则火箭旅行过程中下列说法正确的是( )
A.
火箭要能够降落在1号行星上，则火箭初始出发时最少要携带燃料重量为 85.48
B.
火箭要能够降落在 2 号行星上，则火箭初始出发时最少要携带燃料重量为 1.2
C.
火箭要能够降落在3号行星上，则火箭初始出发时最少要携带燃料重量为 3.76
D.
火箭要能够降落在 4号行星上，则火箭初始出发时最少要携带燃料重量为 10.39
E.
火箭要能够降落在5号行星上，则火箭初始出发时最少要携带燃料重量为 20.16