已知小写字母 b 的ASCII码为98,下列C++代码的输出结果是( )。
#include <iostream>
using namespace std;
int main() {
char a = 'b';
a++;
cout << a;
return 0;
}
b
c
98
99
已知 a 为 int 类型变量,下列表达式不符合语法的是( )。
&a + 3
+a & 3
a - - 4
a++3
下列关于C++语言中指针的叙述 ,不正确的是( )。
指针变量中存储的是内存地址。
指针变量指向的内存地址不⼀定能够合法访问。
结构类型中的指针成员不能指向该结构类型。
定义指针变量时必须指定其指向的类型。
下列关于C++类的说法 ,错误的是( )。
将C++类对象通过值传递给函数参数时 ,会⾃动调用复制构造函数。
将⼀个类的对象赋值给该类的另⼀个对象时 ,不会⾃动调用构造函数。
定义C++类对象时 ,⼀定会调用默认构造函数。
构造派⽣类的对象时 ,⼀定会调用基类的构造函数。
某⼆叉树T的先序遍历序列为:{A B D C E G H F}, 中序遍历序列为: {D B A H G E C F} ,则下列说法中正确的是( )。
T的⾼为5
T有4个叶节点
T是平衡树
以上说法都不对
⼀棵完全⼆叉树有431个结点 ,则叶结点有多少个? ( )
176
215
216
255
下列关于树的说法 ,错误的是( )。
⼆叉树的中序遍历与其深度优先遍历总是相同的。
所有树都可以构造⼀颗⼆叉树与之⼀⼀对应。
如果树的⼀个叶结点有两个不同的祖先结点 ,那么其中⼀个⼀定是另⼀个的祖先结点。
树的结点不能有两个⽗结点。
⼀个简单无向图有10个结点、30条边 。再增加多少条边可以成为完全图 。 ( )
10
15
51
60
以下哪个方案可以合理解决或缓解哈希表冲突( )。
丢弃发⽣冲突的新元素。
用新元素覆盖发⽣冲突的元素。
用新元素覆盖在冲突位置的下⼀个位置。
将新元素放置在冲突位置之后的第⼀个空位。
⼀个迷宫,已知从起点不经过重复结点到达终点的路径有且仅有⼀条,则下面说法错误的是( )。
可以使用深度优先搜索找到这条路径。
可以使用⼴度优先搜索找到这条路径。
该迷宫内与起点连通的结点 ,⼀定也与终点连通。
该迷宫内与起点连通的结点及它们之间的路径可以抽象为无向无环图。
下面C++程序的输出为( )。
#include <iostream>
#include <cmath>
using namespace std;
int main() {
cout << (int)log(8) << endl;
return 0;
}
2
3
8
无法通过编译。
下面C++程序的输出为( )。
#include <iostream>
#define N 10using namespace std;int path[N][N];
int main() {
for (int i = 1; i < N; i++)
path[i][0] = i;
for (int j = 1; j < N; j++)
path[0][j] = j;
for (int i = 1; i < N; i++)
for (int j = 1; j < N; j++)
path[i][j] = path[i - 1][j] + path[i][j - 1];
cout << path[8][4] << endl;
return 0;
}84
495
1012
结果是随机的。
C++程序的时间复杂度为( )。
#include <iostream>
#define N 10using namespace std;int path[N][N];
int main() {
for (int i = 1; i < N; i++)
path[i][0] = i;
for (int j = 1; j < N; j++)
path[0][j] = j;
for (int i = 1; i < N; i++)
for (int j = 1; j < N; j++)
path[i][j] = path[i - 1][j] + path[i][j - 1];
cout << path[8][4] << endl;
return 0;
}
O(1)
O(N)
O(NlogN)
O(N2)
下面 fib 函数的时间复杂度为( )。
int fib_rcd[MAX_N];
int fib(int n) {
if(n<=1)
return 1;
if (fib_rcd[n] > 0)
return fib_rcd[n];
return fib(n - 1) + fib(n - 2);
}
O(n)
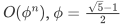
O(2n)
无法正常结束。
下列选项中 ,哪个可能是下图的⼴度优先遍历序列( )。
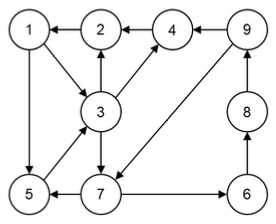
1, 3, 5, 7, 4, 2, 6, 8, 9
9, 4, 2, 1, 3, 7, 5, 6, 8
1, 3, 5, 7, 6, 8, 9, 4, 2
9, 4, 7, 2, 1, 3, 5, 6, 8
表达式 'a ' << 1 的结果为 'a ' 。
在C++语言中 ,函数可以定义在另⼀个函数定义之内。
选择排序⼀般是不稳定的。
埃氏筛法和欧拉筛法都是使用筛法思想⽣成素数表的算法 ,欧拉筛法的时间复杂度更低。
使用math.h或cmath头⽂件中的正弦函数 ,表达式 sin(30)的结果类型为double 、值约为0.5
⼀颗N层的完全⼆叉树 ,⼀定有2N- 1个结点。
⼀个图 ,不管是否连通 ,都可以使用深度优先搜索算法进行遍历。
某个哈希表键值x为整数,H(x) = x % p 是常用的哈希函数之⼀ ,要求 p选择素数是因为这样不会产⽣ 冲突 。( )
使用单链表实现队列时 ,链表头结点作为队⾸⽐链表头结点作为队尾更便于操作。
⼀个图中 ,每个结点表达⼀个人 ,连接两个结点的边表达两个结点对应的人相互认识 ,则这个图可以用来 表达社交⽹络。
小杨寻宝
题面描述
小杨有⼀棵包含n个节点的树 ,树上的⼀些节点放置有宝物。
小杨可以任意选择⼀个节点作为起点并在树上移动 ,但是小杨只能经过每条边⾄多⼀次 ,当小杨经过⼀条边后,这条边就会消失 。小杨每经过⼀个放置有宝物的节点就会取得该宝物。
小杨想请你帮他判断自己能否成功取得所有宝物。
输入格式
第一行包含一个正整数t,代表测试用例组数。
接下来是t组测试用例。对于每组测试用例,一共n+1行。
第一行包含一个正整数n,代表树的节点数。
第二行包含几个非负整数a1,a2,…,an,其中如果ai=1,则节点i放置有宝物,若ai=0,则节点i没有宝物。
之后n-1行,每行包含两个正整数xi,yi,代表存在一条连接节点xi和yi的边。
输出格式
对于每组测试数据,如果小杨能成功取得所有宝物,输出Yes,否则输出No。
样例1

矩阵移动
题面描述
小杨有一个有一个n×m的矩阵,仅包含01?三种字符。矩阵的行从上到下编号依次为1,2,...,n,列从左到右编号依次为1,2,…,m编号。小杨开始在矩阵的左上角(1,1),小杨只能向下或者向右移动,最终到达右下角(n,m)时停止,在移动的过程中每经过一个字符1得分会增加一分(包括起点和终点),经过其它字符则分数不变。小杨的初始分数为0分。
小杨可以将矩阵中不超过x个字符?变为字符1。小杨在修改矩阵后,会以最优的策略从左上角移动到右下角。他想知道自己最多能获得多少分。
输入格式
第一行包含一个正整数t,代表测试用例组数。
接下来是t组测试用例。对于每组测试用例,一共n+1行。
第一行包含三个正整数n,m,x,含义如题面所示。
之后n行,每行包含一个长度为m且仅包含01?三种字符的字符串。
输出格式
对于每组测试用例,输出一行一个整数,代表最优策略下小杨的得分最多是多少。
样例1
