一张棋盘由n行 m 列的网格矩阵组成,每个网格中最多放一颗棋子。当前棋盘上已有若干棋子。所有水平方向或竖直方向上相邻的棋子属于同一连通块。
现给定棋盘上所有棋子的位置,如果要使棋盘上出现两个及以上的棋子连通块,请问最少需要移除几颗棋子?如果无论怎么移除棋子都无法满足要求,则输出 -1。(注:只能通过移除棋子的操作来使棋盘上出现两个及以上的棋子连通块。
由下图可知,最少需要移除 2颗棋子才能使棋盘上出现两个及以上的棋子连通块。移除后棋盘示意图如下:
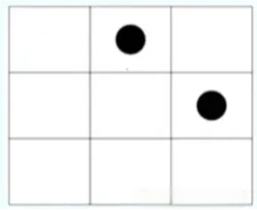
例如:n=3,m=3,3x3的棋盘示意图如下:
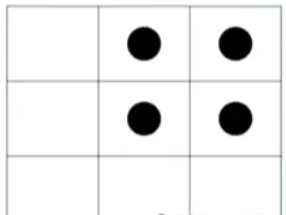
故答案为 2。
输入格式
本题每个测试点包含多组测试数据第一行包含一个整数T(1≤T≤50),表示数据组数接下来T组数据,每组数据第一行输入两个整数 和 m(1≤n,m≤60),分别表示组成棋盘的网格矩阵的行数和列数,整数之间以一个空格隔开
接下来 n 行,每行输入m 个大写字符(字符为'G'或'L'),分别表示每个网格的情况,’G’表示有棋子,'L'表示无棋子,字符之间以一个空格隔开
输出格式
输出T行,每行一个整数,第i行的整数表示第i组数据中最少需要移除多少颗棋子才能使棋盘上出现两个及以上的棋子连通块;如果无论怎么移除棋子都无法满足要求,则输出 -1。
输入样例
2 3 3 L G G L G G L L L 4 4 L L L L L G L L L G L L L L L L
输出样例2
-1